What are Binary Search Trees (BST)?
BST is a type of tree data structure that organizes data in a sorted order. Data are stored in nodes, which holds references to other nodes. So BSTs are essentially a collection of nodes that have references to one another, similar to a Graph. In fact BSTs can also be considered a Graph data structure, but when you look for examples of graphs, it almost looks nothing like a tree. The reason being is because trees are a bit more unique.
In trees, there is a root node, this is a node in which all other nodes are extended from. All paths of a node will lead to the root node and vice versa, a root node will have a path to all other nodes.
What is a node?
A question you may be wondering is, what is a node? For Binary Trees, you can think of nodes as an object with 3 properties, a value, a left branch, and a right branch. Value represents an assigned data or identifier to that particular node, as a number (usually a number), a letter, a symbol, etc. These values may not be unique, at least for Binary Trees, but for Binary Search Trees (yes, there is a difference between the two even though the names are almost identical), they usually are.
That is what a value represents and as for the branches, the left branch represents a reference to another node and so does the right branch. A node can extend to two other nodes via branches. The node with a left or right branch that extends to another node is known as the parent node. The node that is being extended from is known as the child node. Thus you can think of the properties, left and right branch as just references.
What is a branch?
A branch is a one way connection to nodes. Think of linked lists, Each node will have a reference to the next node until there is no next node or when a null value is reached. So in an example with the parent node, it will have a reference to the child node, but the child node will not have a reference to its parent node. The child node can have its own children node, making them its parents. It'll also build that same connection and it can keep on going. A node that does not extend to any nodes from either branches or in other words if its left and right branches are null, then it'll be known as a leaf node. If all that sounds a bit confusing, no worries, I'll provide some examples and further details.
Example of a BST
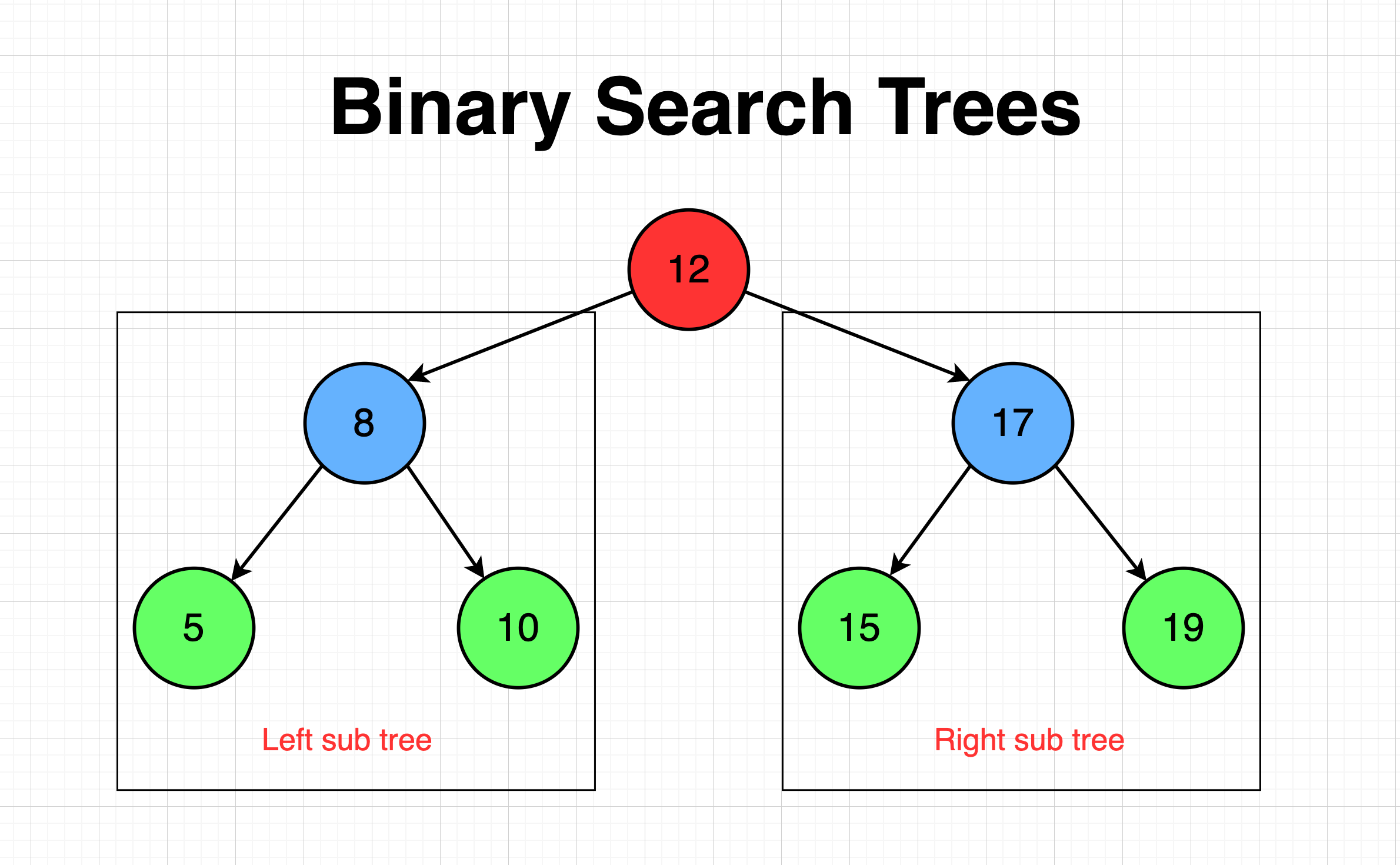
In the image above, you'll see an example of a BST. I've color coded it, added some arrows, and organized it to try to make it as straightforward and simple to understand as possible. I'll go over what it all means.
Each circle represents a node, the number in each of the nodes represents its values. The arrows represents a branch. The red node is the root node, the blue is a parent, and the green is a leaf node. For clarifications, the blue nodes can also be a child node, nodes 8 and 17 are the child node of node 12. And again, a leaf node does not have any children. The branch only goes in one direction as represented by the arrow, so for example node 12 will have references to node 8 and 17. Specifically, its left value will represent node 8 and its right value will represent node 17. Nodes, 5, 10, 15, 19 don't have any branches, which means that it's left and right values are null.
What are subtrees?
Subtrees are essentially just a smaller portion of a whole tree. In the image above you can see an example of the left sub tree and the right subtree. Remember when I mentioned that a node's left value is a reference to another node? Well I forgot to mention that a node can also be referred to as a tree node or just a tree. So each node that you see on the tree is a tree of its own, even the leaf nodes. How many sub trees are in the BST above, excluding the root node (the root node is not a sub tree because it can traverse down to all nodes in path, it more so represents a whole tree)? If you said 6, then you are correct!
Implementation of BST
Hopefully I've done a pretty good job in explaining what a BST is, and now let's shift our focus to implementing one. Implementing a BST is actually pretty simple and short, it requires 2 functions, one function is to create a node, and the other function is to set the the start of the tree or the root node. Let's first start off with creating a node.
function Node(data, left = null, right = null) { this.data = data; this.left = left; this.right = right; }
As I've mentioned previously, a node has 3 properties, the value or data, a left branch and a right branch. The left and right branch values will have a reference to another node. If it doesn't have a reference to any other nodes, then by default, it should be set to null. That is all for the Node function. The function to set the root node is even simpler.
function BST() { this.root = null; }
That is all for the function to set the root node. This function is where it all starts, to begin the construction of the tree. Once you have created this two functions, congratulations! You have created your first BST. But you may be wondering what do I do from there? Well, let's recreated the BST image example above with these functions.
Constructing BST
The process I'm about to show you is going to be pretty long and tedious and there is a more efficient and better way of doing it, but let's stick with it. It'll really help you conceptualize the whole paradigm of a BST, and once you understand it, we can then start going over the more advanced topics. So let's start off first by creating a new BST.
const bst = new BST();
This will be the start of our tree, we need to assign it a root node, but since we haven't created any nodes yet, we can skip the assignment for now. Instead let us now focus on creating the nodes. There are a total of 7 nodes in the diagram above, so let's create all 7 of them.
const node12 = new Node(12); const node8 = new Node(8); const node17 = new Node(17); const node5 = new Node(5); const node10 = new Node(10); const node15 = new Node(15); const node19 = new Node(19);
These are the 7 nodes from the example BST image above. We haven't assigned the left and right branch values just yet because the goal is to first create the nodes, and then start assigning values. Remember, a left and right branch value will have reference to another node, so we will be assigning the nodes created to each other. Let's first assign the root node and then go from there by following the diagram.
bst.root = node12; node12.left = node8; node12.right = node17; node8.left = node5; node8.right = node10; node17.left = node15; node17.right = node19;
That is all, we have fully implemented the example BST above. If you console.log the bst variable, you should see the coded up version of the structure of the BST, where it displays the data, left and right values of all the nodes.
Insertion Function
Creating and assigning nodes like we've done in the previous section is repetitive and tedious especially for larger trees. Let's automate that whole process by creating an algorithm to make it much more efficient.
Completed
Hopefully this post helped you understand what a BST is and how to implement one. This is all just a quick basic, but it may not be enough to really grasp it. There are a few important algorithms that you need to know to really help you grasp this data structure. The first being the insert function, which basically inserts a node to the tree, and the other 4 (yes, four) are traversals. These traversals are the pre-order, in-order, post-order, and level order traversals. I will be going over all these algorithms in later posts. But all in all I really do hope this post helped you with the core basics.
